Beim Ableiten oder Differenzieren geht es darum, die Steigung einer Funktion zu bestimmen.

 

Denken wir zurück an das Kapitel "Lineare Funktionen / Geraden":

Jede lineare Funktion kann man in der Form y = mx + t schreiben,

wobei wir m als die Steigung bezeichnet haben.

Wer sich noch erinnert weiß:

• Geraden mit positiver Steigung steigen von links nach rechts
• Geraden mit negativer Steigung fallen von links nach rechts
• Je größer die Steigung, desto steiler verläuft eine Funktion

 

Genauso wie Geraden, haben alle anderen Funktionen, also z.B. Parabeln oder ganzrationale Funktionen ebenfalls eine Steigung.

Einziger Unterschied: die Steigung ist nicht immer gleich, sondern ändert sich, je nachdem an welcher Stelle der Funktion man gerade ist.

 

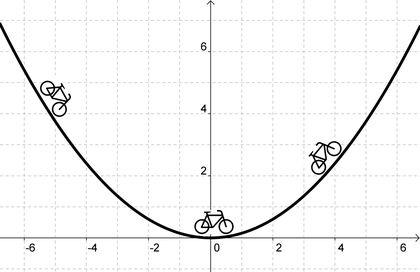
Stellt euch am Besten folgendes vor: die Funktion stellt den Höhenverlauf einer Strasse dar, die ihr mit dem Fahrrad von links nach rechts fahrt. Dann seht ihr am folgenden Bild:

• Erst geht es steil bergab ( = negative Steigung)
• In der Mitte ist es kurz flach ( = Steigung gleich Null )
• danach geht es immer steiler bergauf ( = positive Steigung )

 

Mathematisch bestimmt man die Steigung einer Funktion durch "Ableiten". Bei den ganzrationalen Funktionen ist das ein sehr einfaches Verfahren:

 

Beim Ableiten wird der Exponent der Variablen x um eins reduziert und der ursprüngliche Exponent vor die Variable geschrieben.

 

     Also wird aus   x²    ->  2x

                     aus   x³    ->  3x²

                     aus   x^4 ->  4x³

                             usw. ...

Ein x entspricht x¹ also: x¹    ->   1

 

Beachte:

• Eine Zahl ohne x fällt beim Ableiten ganz weg!
• Zahlen vor dem x, x² usw. bleiben erhalten, z.B. 5x² -> 2·5·x = 10x

 

Hat man eine Funktion f(x), dann führt man dieses Verfahren einfach Schritt für Schritt mit jedem Teil der Funktion durch:

 

                                       f   (x) = x² + 5 x - 3

Dann ist die Ableitung    f ' (x) = 2 x + 5

 

 

Noch ein Beispiel:         g   (x) =   x³ +   4 x² -  x  +  2

Ableitung:                      g ' (x) = 3 x ² + 4·2·x  - 1

                                                 = 3 x² + 8 x  - 1

 

 

 

Aufgaben:

Bestimme für folgende Funktionen jeweils die Ableitung:

a) p (x) = 8x²

b) q (x) = 9x + 4

c) f (x) = x³ - 4x² - 2x + 0,5

d) g (x) = x³ - 3x² - x

e) k (x) = (7x - 9) (x + 1)

 

Die Lösungen findet ihr hier:  >> LÖSUNGEN <<