FOS-Mathetrainer.de
Nullstellen:
Eine Ganzrationale Funktion kann so viele Nullstellen haben wie ihr Grad beträgt. Das heißt eine Funktion 3.Grades kann auch maximal drei Nullstellen besitzen.
Nullstellen sind nichts anderes als Schnittpunkte mit der x-Achse. Deshalb muss man beim Suchen der Nullstellen die Gleichung f(x) = 0 lösen.
Mit anderen Worten: Für welche x-Werte ist das Ergebnis der Funktion Null?
Um die Nullstellen zu bestimmen gibt es verschiedene Methoden:
- x Ausklammern
Diese Methode funktioniert wenn in jedem Teil des Funktionsterms mindestens ein x steckt. Also z.B. bei
f(x) = x³ - 2x
Den Rechenweg findet Ihr im Kapitel Nullstellen mit x Ausklammern
- Erraten einer Nullstelle
Nehmen wir zum Beispiel die Funktion f(x) = x³ - 2x² - x + 2
Wir suchen die Lösung der Gleichung 0 = x³ - 2x² - x + 2
Dazu setzt man testweise ein paar kleine, ganze Zahlen wie 0, 1, 2, -1, ... für x in die Funktion ein. Ist das Ergebnis Null, so hat man eine Nullstelle gefunden.
Versuchen wir das mit der Funktion f(x):
x = 0 Einsetzen: f(0) = 0³ - 2 · 0² - 0 + 2 = 2
x = 1 Einsetzen: f(1) = 1³ - 2 · 1² - 1 + 2 = 0
Bei x = 0 ist also keine Nullstelle, aber bei x = 1 ist eine! So haben wir die erste Nullstelle der Funktion gefunden. Die nächste können wir mithilfe der Polynodivision berechnen.
- Berechnen mit Polynomdivision
Wenn man schon eine Nullstelle kennt kann man die weiteren Nullstellen ausrechnen. Dazu muss man die Funktion f(x) durch den Linearfaktor (x - 1) (also "x minus erste Nullstelle") teilen.
Das macht man mit der Polynomdivision:
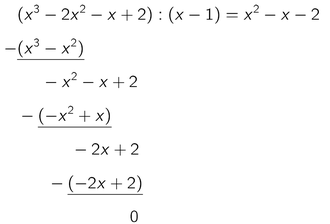
Das Ergebnis ist also: x² - x - 2
Das Ergebnis setzt man in die Mitternachtsformel ein:
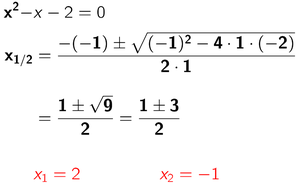
Wir haben also insgesamt drei Nullstellen: Bei x = 1, x = 2 und x = -1
Die Nullstellen sieht man auch am Graph der Funktion, nämlich dort, wo er die x-Achse schneidet: